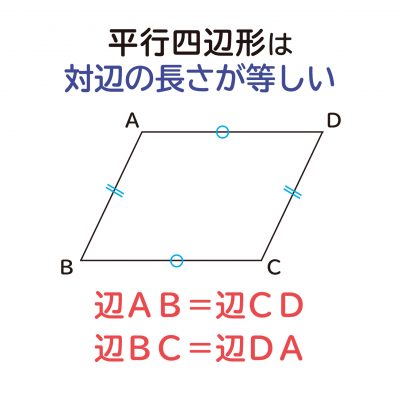
平行四辺形 対角線 角度Ao=co (平行四辺形の対角線はそれぞれの中点で交わる) ∠aoe=∠cof (対頂角) ∠eao=∠fco (ab//cd 錯角) 1組の辺とその両端の角がそれぞれ等しいので aeo≡ cfo 合同な三角形の対応する辺は等しいので ae=cf ∠def=∠bef (折り返した角) ∠def=∠efb 平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 「 2本の対角線が垂直 ( 90° ) に交わる 」 と言う2つの条件が加われば、正方形になります。 正方形、長方形、ひし形はいずれも平行四辺形であり、平行四辺形の中でも、一定の条件を追加しImage 平行四辺形 対角線 長さ 求め方 7734平行四辺形 対角線 長さ 求め方 していく。また、平行が何組あるか、辺の長さや角の大きさ、対角線の長さ や位置関係に着目して様々な四角形を観察する中で、図形の性質について考 察して

平行四辺形について知ろう 苦手な数学を簡単に
平行四辺形 対角線 角度 求め方
平行四辺形 対角線 角度 求め方- 構築された対角面を見つけます。 それは別の直角三角形b、c、nの斜辺です。 ピタゴラスの定理によれば、n 2 = c 2 + b 2である。 式を計算し、結果の値の平方根を取ります。これは面nの対角になります。 4 平行六面体mの対角線を求めます。 ミニログハウスの基礎工事で、四辺の直角を出すために対角線の長さを調べました。 純文科系なので数学は絶望的に弱く、大変助かりました。 1406




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
平行四辺形の対角線の長さの求め方がわかる4ステップ 平行四辺形ABCDにおいて、AB = CD = 6cm、AD = BC = 10cmとする。 角A = 1°のとき、対角線ACの長さを求めよ。 をときながら解説していくよ。 つぎの4ステップでとけちゃうんだ。 Step1 「頂点」から垂線をおろす 平行四辺形の頂点から垂線をおろそう。平行四辺形の性質について確かめましょう。 ※「向かい合う辺の長さは等しい」「向かい合う角の大きさは等しい」 平行四辺形の性質や,平行線のかき方を使って平行四辺形をかく学習は, 4年生単元「垂直・平行と四角形」で学習しています。 次に、平行四辺形の角度や対角線の長さを求める方法を、以下の例題で解説していきます。 例題 平行四辺形 \(\mathrm{ABCD}\) において、\(\mathrm{AB} = \mathrm{CD} = 6 \ \text{cm}\)、\(\mathrm{AD} = \mathrm{BC} = 8 \ \text{cm}\) とする。
平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から)(1)下の図について,ア,イの角度を求めなさい。 ① ② (2)下の図の三角形について,ウ,エの角度を求めなさい。 ① ② (3)下図の平行四辺形ABCDについて,オ,カの角度を求めなさい。 (4)下の図の二等辺三角形について,キの角度を求めなさい。 平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを 平行四辺形の対角線の角度について この条件の時の角度a B
平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。− 76 − 高校講座・学習メモ ベーシック数学 24 平行線に関すること 問題2 右の図において,l//m のとき, ∠xと∠y の大きさを求めなさい。平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。 分かり易いところなので得点しやすいですが、理解していないと大きな差となります。 落とせないところなのでいくつかの出題パターンを確認しておきましょう。 1




平行四辺形の定義と性質 証明問題の解き方 数学fun




中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo
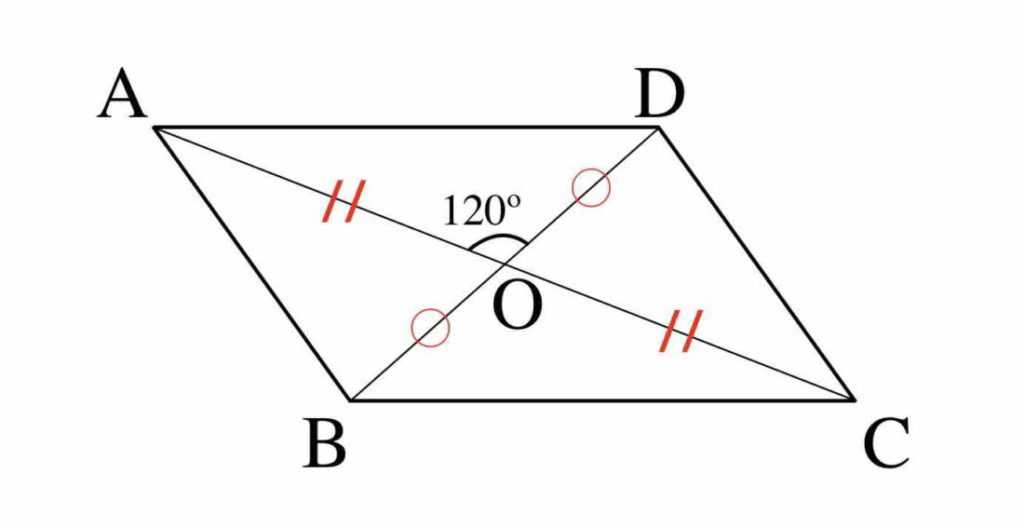
平行四辺形の対角(向かい合う角度)の大きさは、それぞれ等しくなります。 平行四辺形の対角線は中点で交わる 平行四辺形に対角線を引くと、2つの対角線が交わる点が、それぞれの対角線の中央にきます。 上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積平行四辺形 対角線 角度 求め方③ 平行四辺形の対角線は,それぞれ中点で交わるので,oa=oc,od=bd÷2 5 問題 (3 学期) 次の平行四辺形abcd で,①~③の長さや角の大きさを求めよ。 平行四辺形の対角線の求め方を教えてください 農場長 平行四辺形の面積を対角線と角度から求める問題 Youtube 平行四辺形の対角線を3つに分けるならチョウチョを2




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
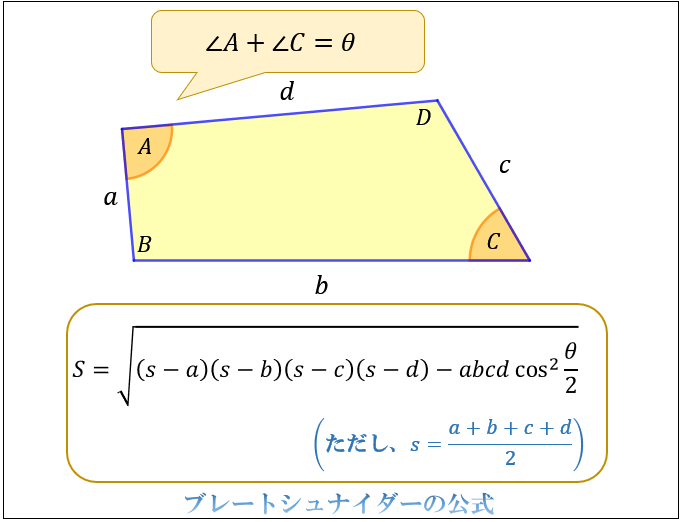
(1)平行四辺形や三角形の面積の求め方を理解し,それらの面積を求めることができる。 (2)いろいろな平面図形の面積について,既習の図形の面積の求め方を基に考えたり,活用したり する能力を高める。 平行四辺形や三角形などの面積を求めるときに たとえば、「4辺の長さがそれぞれ 5, 15, 8, 12 で1組の対角の和が 150 ° の四角形」の面積は、ブレートシュナイダーの公式を使うことで 30 30 3 ≒ 8196 と求まります。 ただし、 ∠ A と ∠ C の角度がそれぞれ分かっている場合は、 三角形の面積の公式 を それぞれの特徴を比較! そもそも平行四辺形とは このように 向かい合う辺がそれぞれ平行になっている四角形 のことを平行四辺形といいます。 更に、次のような条件を満たす四角形はすべて平行四辺形ということができます。 平行四辺形になるための条件 2組の対辺がそれぞれ平行である。 2組の対辺がそれぞれ等しい。 2組の対角がそれぞれ等しい



1
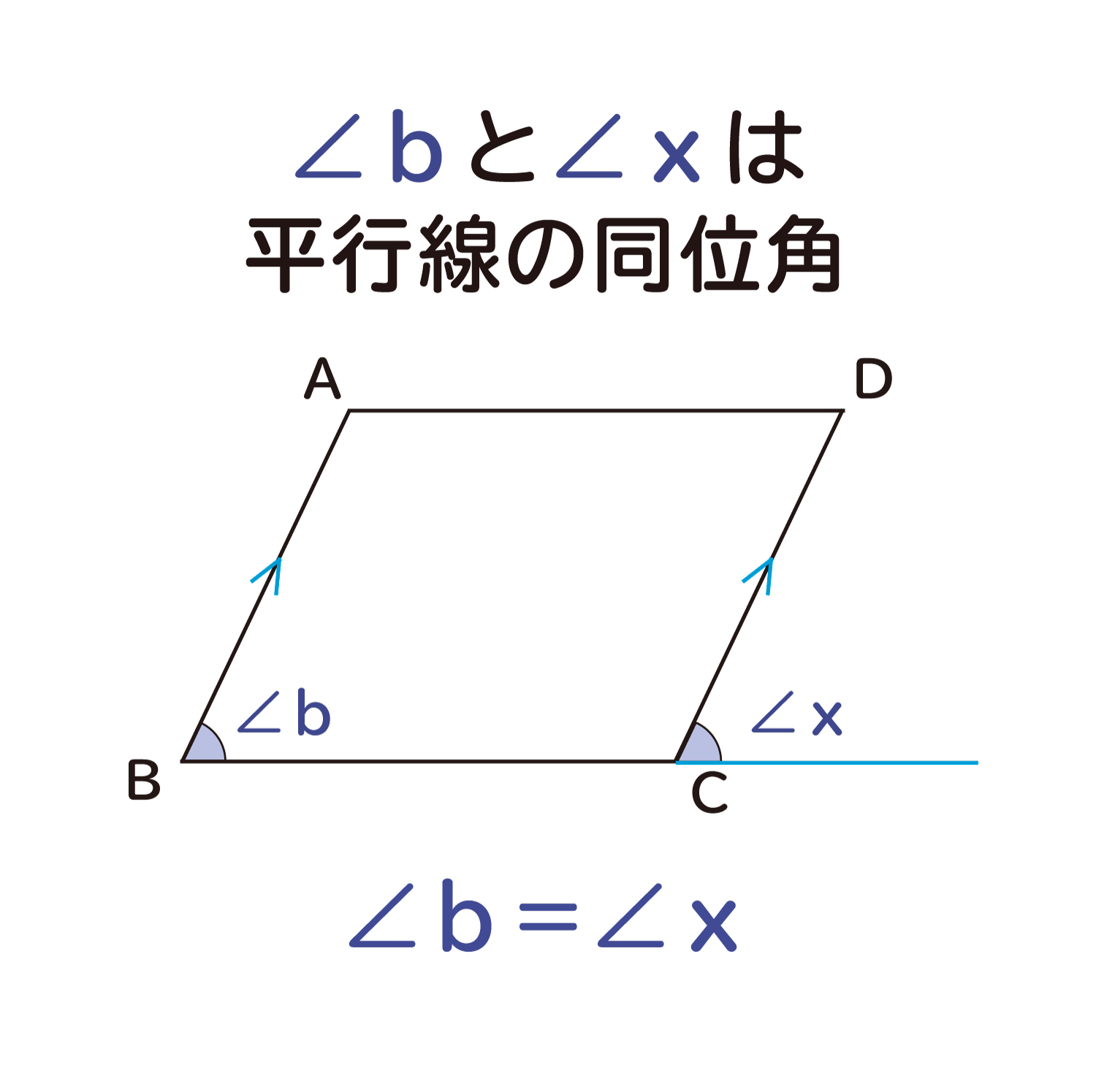



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル
平行四辺形 の性質 ①2組 ③2組の向かい合う角はそれぞれ等しい ④対角線は互いに他を2等分する 10 三角形の辺と平行線 11 18 1つの角が等しい三角形の面積比 19 相似形の面積比 三平方 このようになるには,四角形EBFDが長方形になるしかありません. ゆえに, BDFにおいて DF=DB/2=1・・・⑥ ところで,錯角の関係から ∠ACF=∠DAC=15°・・・⑦ ∠AOE=∠EOB∠AOB =60° (15°30°) ← AODの内角と外角の関係 =15° であり対頂角から ∠FOC=15°・・・⑧ となるので,⑦⑧より FOCは二等辺三角形なので FO=FC=1・・・⑨ ⑥⑨から DFCは直角二等辺三角形例題 平行線の錯角、同位角 例題 図で、l//mのときxの角度を求める。 63° 42° x l m 解き方 63°の錯角、42°の同位角をそれぞれ図示する。 63°の錯角 42°の錯角 直線は180°なので、1=75° 75° これはxの対頂角なので x = 75° 63° 42° x l m 42° 63° 75° 確認l//mのときxの角度を



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




ボード 勉強 のピン
台形 対角線 対角線が直交しない場合はどうすればよいでしょうか 実は対角線が直角に交わらない場合でも対角線の長さと面積の間には関係がありますただし高校数学で習う三角比の考え方が必要です どんな四角形でも対角線のなす角を theta とおくと長方形,正方形,台形,平行四辺形,ひし形の対角線の長さや交わり方について,次のア, イ,ウにあてはまるものを選び, を書きましょう。 長方形 正方形 台形 平行四辺形 ひし形 ア 2本の対角線の長ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。




印刷 平行四辺形 対角線 角度 求め方 平行四辺形 対角線 角度 求め方




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
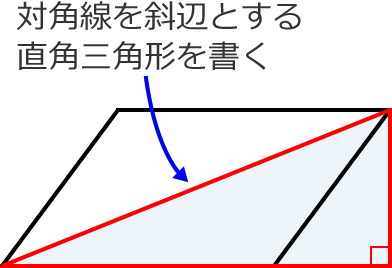
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し平行四辺形の面積を対角線の長さと角度から求める $2$ つの対角線の長さが $4$ $6$ 、その2辺のなす角が $60 $ のとき、その平行四辺形の面積を求めよ 対角線は他の対角線の中点で交わるってことを利用して、図にするとこうなるね四角形ABCDにおいて対角線の交点をOとします。 AB//DC、AD//BCのとき、「AB=DC、AD=BC」であること、「∠BAD=∠DCB、∠ABC=∠CDA」であること、「AO=CO、BO=DO」であることを示します。 ABDと CDBにおいて、 仮定よりAB//DC、AD//BCであり平行線の錯角は等しいので、 ∠ABD=∠CDB・・・① ∠ADB=∠CBD・・・② BDは共通・・・③ ①②③より1組の辺とその両端




平行四辺形の辺や角を求める Youtube




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
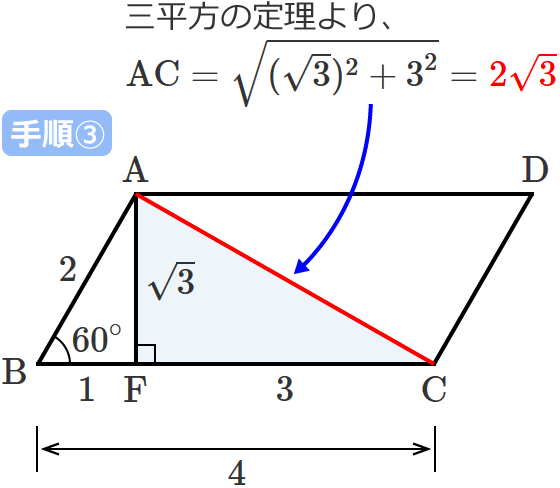



平行四辺形の対角線の長さの求め方




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
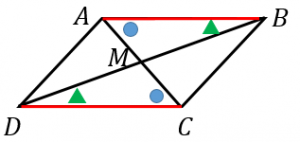



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
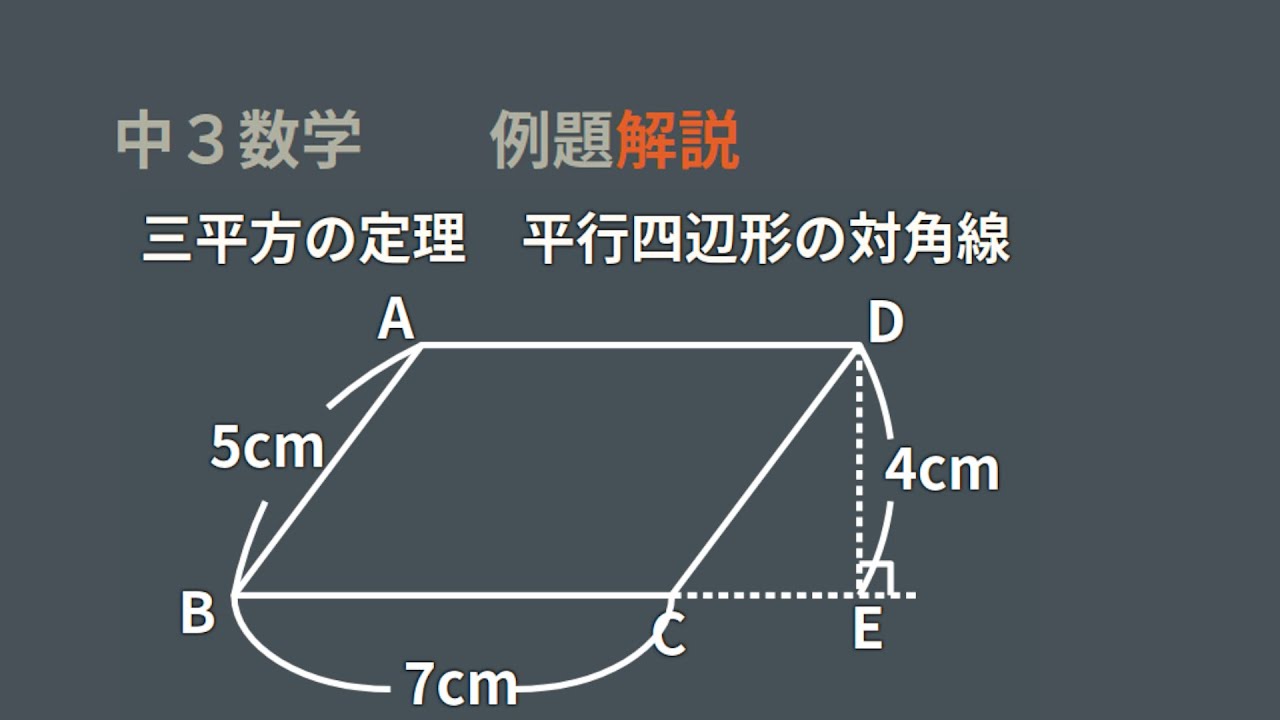



三平方の定理 平行四辺形の対角線




小4算数 Aと同じ角度はどれ 垂直と平行といろいろな四角形 台形 平行四辺形 ひし形 の解き方 教え方 いっしょに勉強しよ




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




印刷 平行四辺形 対角線 角度 犬 イラスト
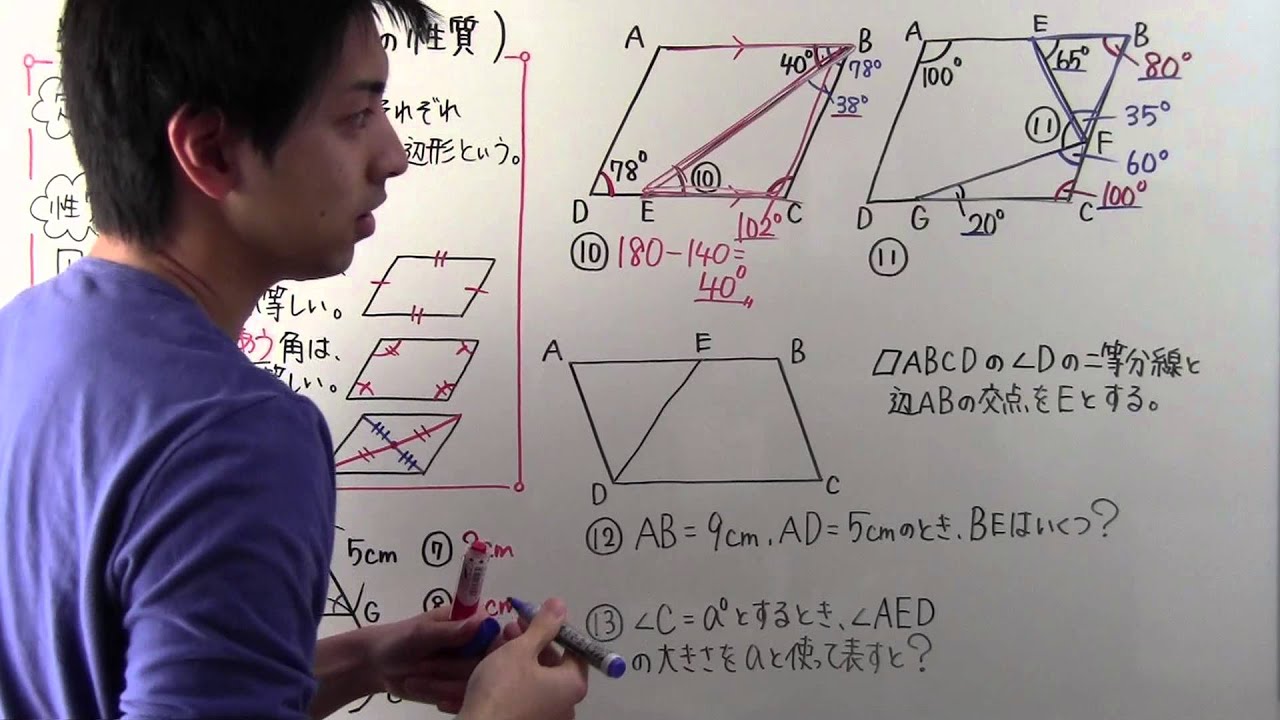



数学 中2 73 平行四辺形の性質 Youtube




平行四辺形の面積を対角線と角度から求める問題 Youtube




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会
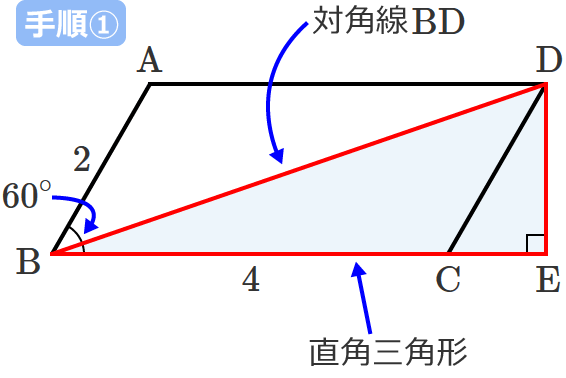



平行四辺形の対角線の長さの求め方




印刷 平行四辺形 対角線 角度 求め方 平行四辺形 対角線 角度 求め方




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学



1




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




平行四辺形の辺や角を求める Youtube




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



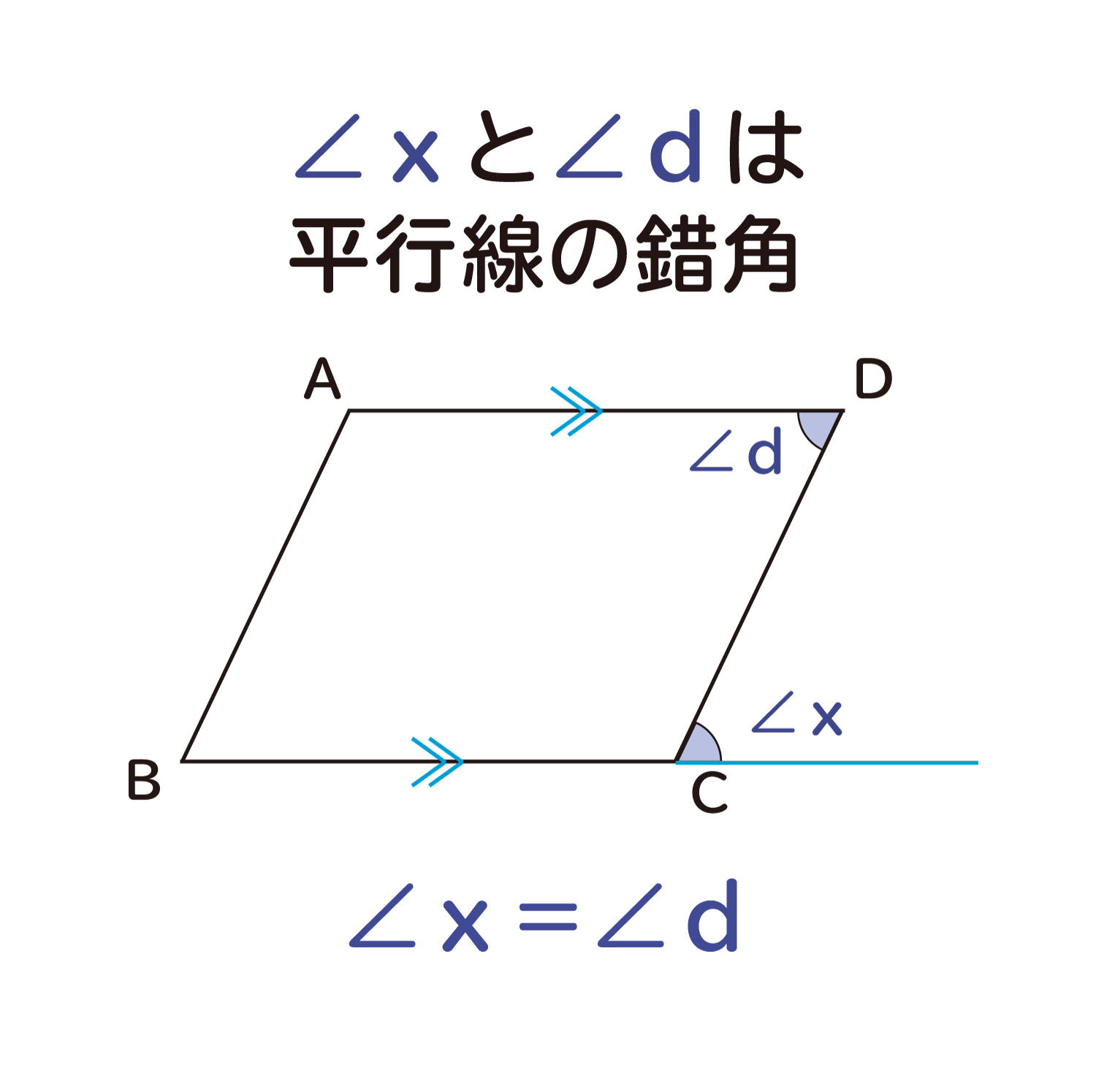
印刷 平行四辺形 対角線 角度 求め方 平行四辺形 対角線 角度 求め方



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル
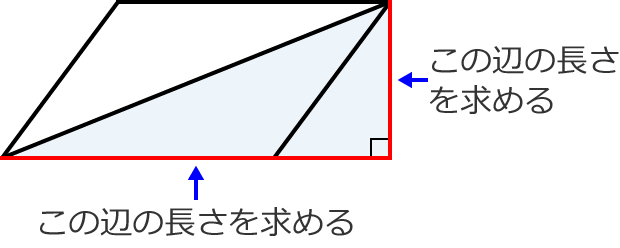



平行四辺形の対角線の長さの求め方




四角形の4辺の長さと対角線のなす角がわかっている時 対角線の長さを 数学 教えて Goo




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形で知っておくべきこと 苦手な数学を簡単に
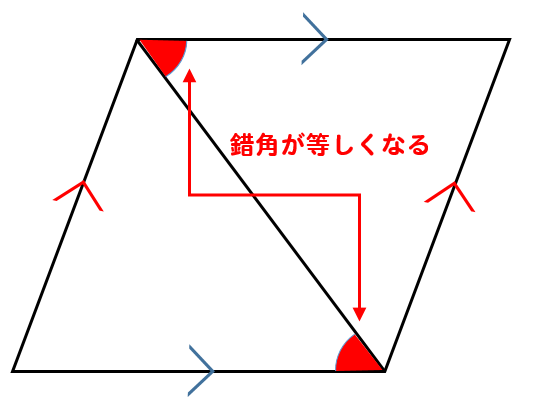



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



4年算数 垂直 平行と四角形 2 教え方



平行四辺形対角線の求め方と面積について 対角線acの長さの Yahoo 知恵袋
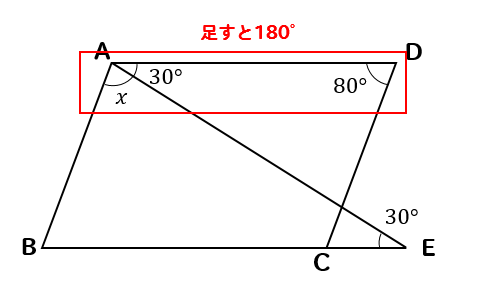



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
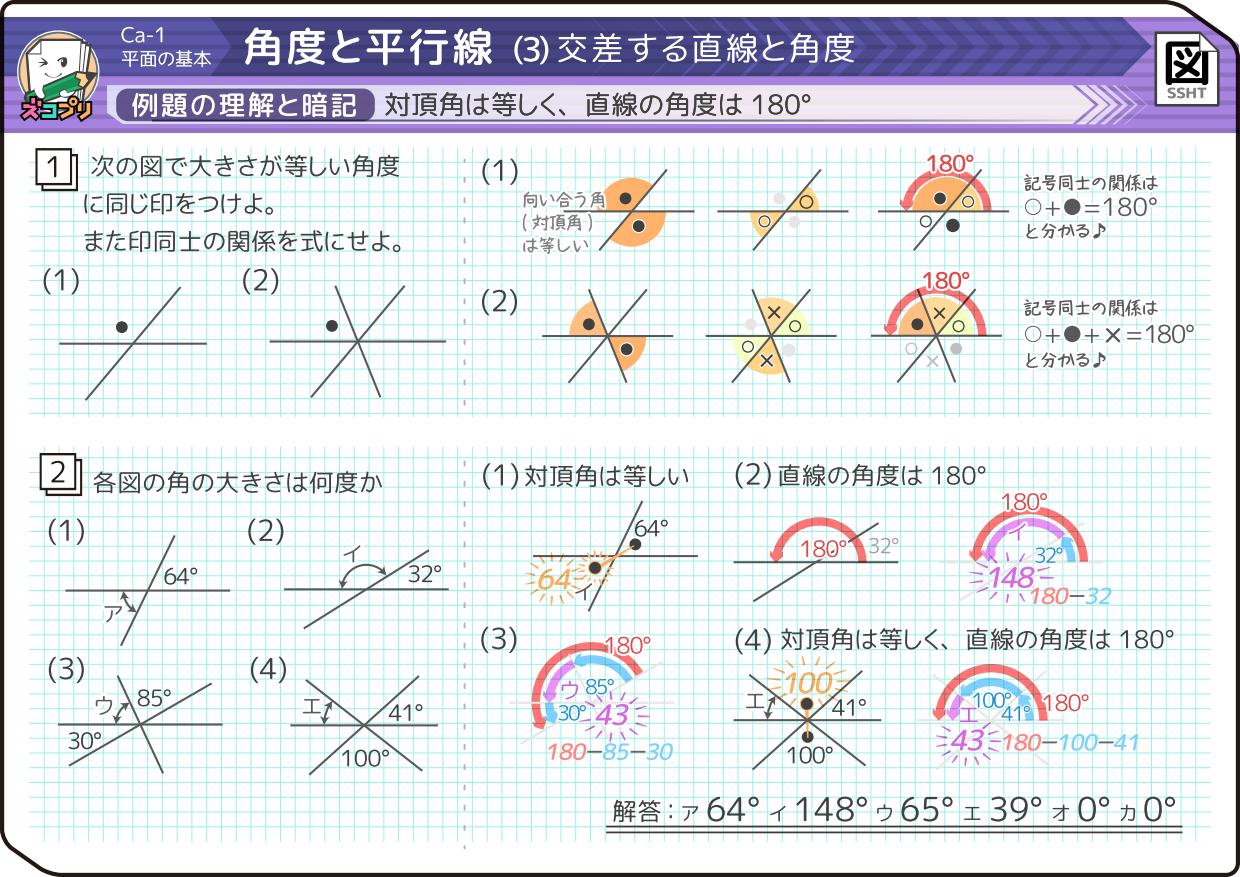



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



平行四辺形の対角線の角度について この条件の時の角度a Bを文字で表 Yahoo 知恵袋




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
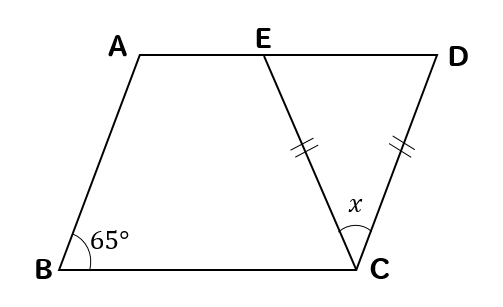



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形について知ろう 苦手な数学を簡単に



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の対角線の長さの求め方



平行四辺形の対角線の長さの求め方



平行四辺形と角度 中学から数学だいすき



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の面積の求め方 公式と計算例
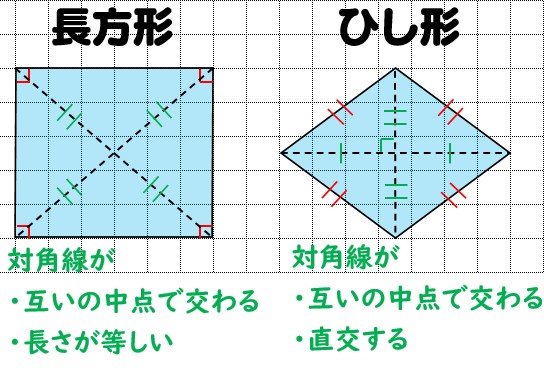



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



三角比を用いた面積計算をマスターしよう スタディクラブ情報局




対角線と四角形 Youtube




平行四辺形の対角線の長さの求め方




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



平行四辺形の角の求め方がわかりませんお願いします 四角形 Yahoo 知恵袋




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



1




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



角を求める問題




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
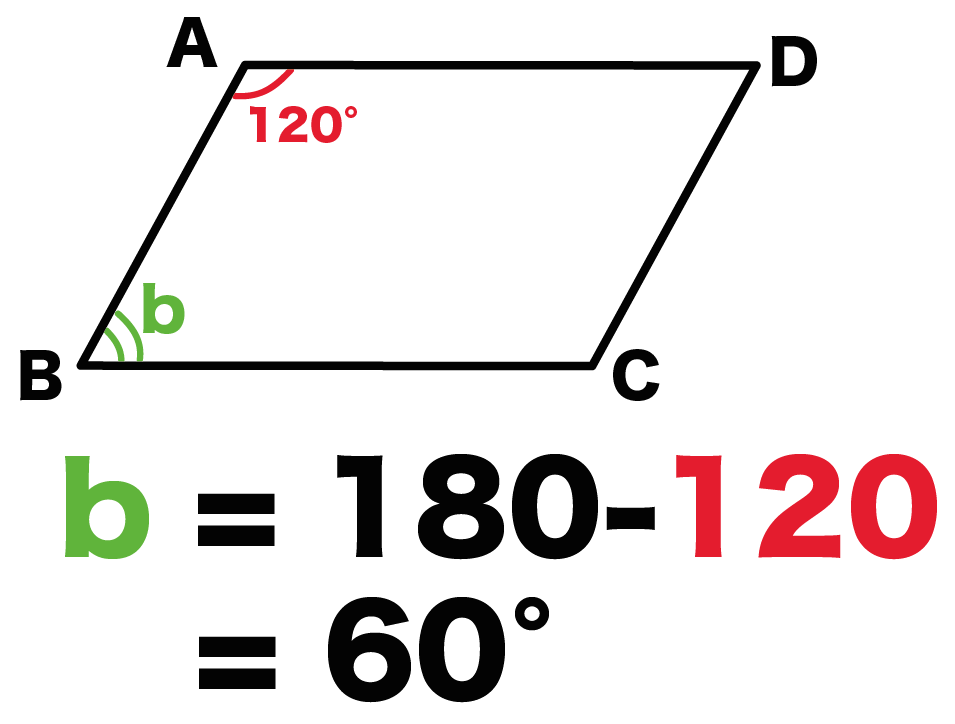



簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
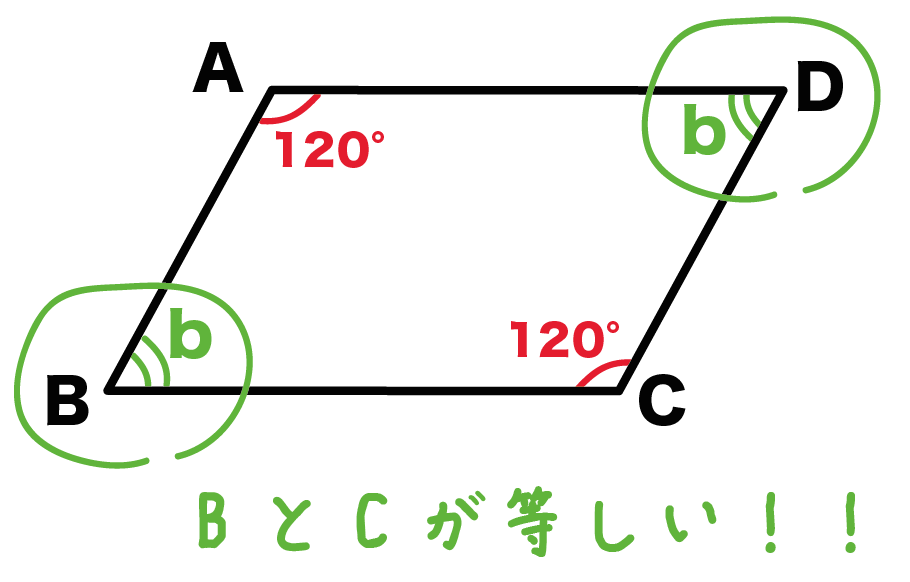



簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2数学 平行四辺形の性質 練習編 映像授業のtry It トライイット




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
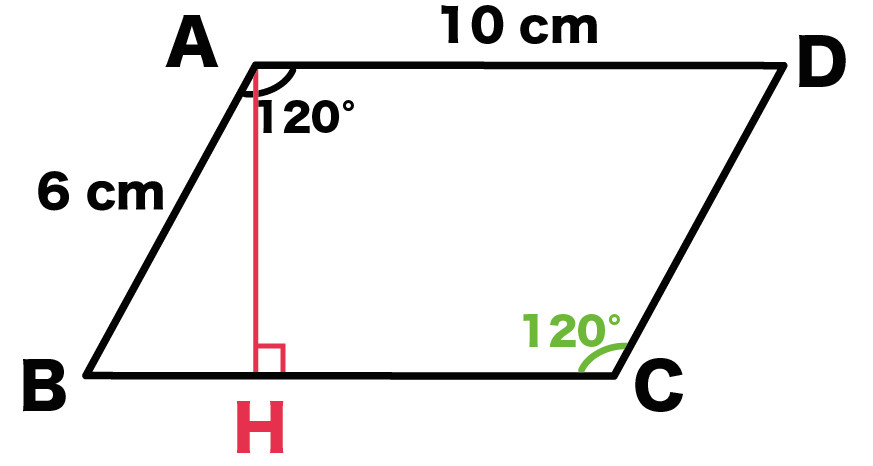



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
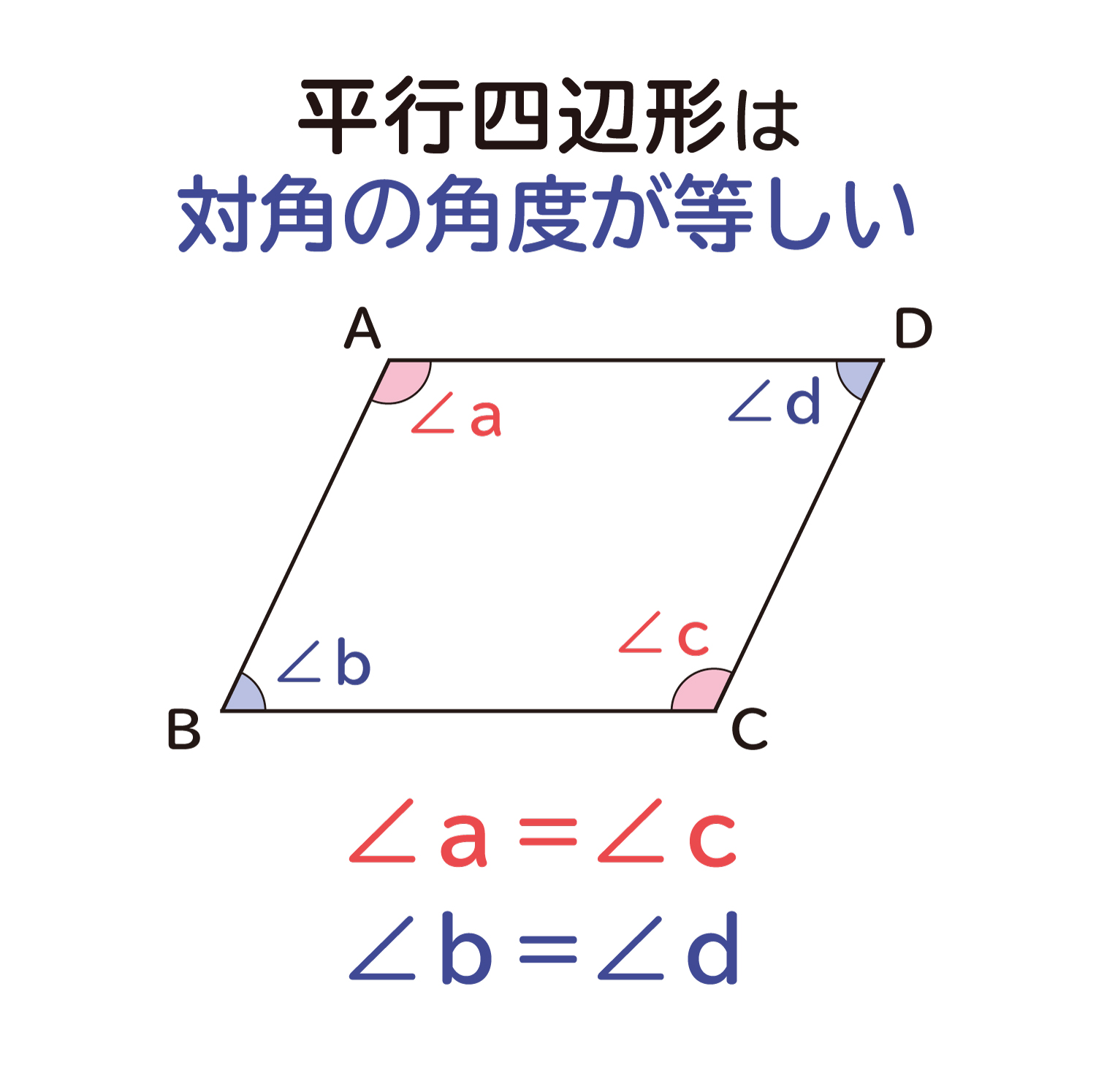



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル



4年算数 垂直 平行と四角形 2 教え方



平行四辺形の法則とは 1分でわかる意味 計算 証明と角度の関係



平行四辺形の角の求め方がわかりませんお願いします 四角形 Yahoo 知恵袋



平行四辺形の角の二等分線
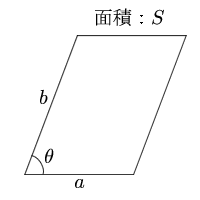



平行四辺形 2辺と間の角度 面積の計算 計算サイト




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



平行四辺形abcdについてcabの角度求め方を教えて下さい Yahoo 知恵袋




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



1




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
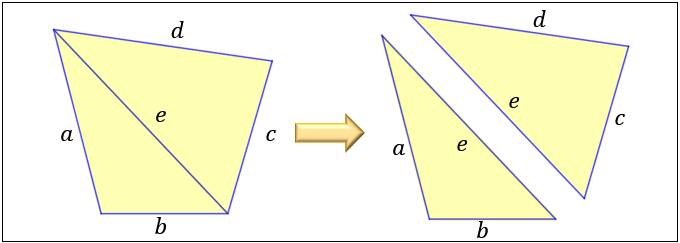



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




平行四辺形の面積 2辺と夾角から 高精度計算サイト



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




パズルから数学へ




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント



0 件のコメント:
コメントを投稿