底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3} Sh V = 3 1 S h の導出を紹介します。 目次 特殊な四角錐の場合 一般の錐体の場合 積分を用いた証明 特殊な四角錐の場合 底面が一辺 2 h 2h 2 h の正方形であるような特殊な正四角錐の場合は,立方体を六個に 半球の表面積を求める問題では、半球の底の部分の足し忘れに注意しましょう! 半球の底の面積 = 3×3×π = 9π・・・② よって、この半球の表面積は、 ① ② = 18π 9π = 27π・・ となり、三角形の面積の公式が求められました。 関連記事 数学の疑問 内積とは何なのか?ベクトルの内積の2つの求め方とその活用法 18年5月25日 Tooda Yuuto アタリマエ! 数学の疑問 三角比・三角関数の公式一覧。正弦・余弦・加法定理など 17年7月3日 Tooda Yuuto アタリマエ! 数学の疑問

4种方法来计算三角柱的表面积
底面積公式
底面積公式-よって 側面積 は、1辺が $ 6\pi $、もう1辺が円柱の高さ $4$ の 長方形の面積 より、$ 6\pi \times 4 = 24\pi $ と求まります。 あとは、 底面積 と 側面積 を足すだけです。ただし、底面は2つあるので、底面積を2倍するのを忘れないようにしましょう。立体の体積&容積および諸数値 V=容積、S=表面積、As=側面積、Ab=底面積、x=底面より重心までの距離 寸 法 容積および諸数値 寸 法 容積および諸数値 V=a 2 S=6a 2 As=4d 2 正多角形 a=辺長



1
2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 角すいと円すいの体積=底面積×高さ× 1 3 角すいと円すいの表面積=底面積側面積 4円すい正方体的底面积=棱长x棱长 所以,长方体和 正方体 的体积也可以这样来计算: 长方体(或正方体)的体积=底面积x高 如果用字母s表示底面积,上面的公式可以写成: v=sh直円錐を斜めに切断した体積と切断面積と底面積を計算します。 一部が欠けた直円錐の体積 一部が欠けた直円錐の体積 直円錐の半径と高さから縦に切断した体積、底面積、側面積、切断面積を計算しま
三角錐の体積=底面積×高さ/3 です。 底面の形が円の円錐でも、底面を小さな三角形の総和であると考えれば、 三角錐の公式が使えるので、 円錐の体積=底面積×高さ/3 になることがわかります。 (別の例) 上図のように、立方体を考えます。土量算出公式と体積の確認 7 0849 50歳代 / エンジニア / 非常に役に立った / 角錐台の底面積と上面積と高さから体積を計算します。 ゲストさん;V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式
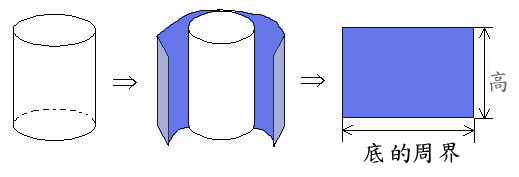
底面積は\(6\times 6\times \pi=36\pi (cm^2)\) 円周の長さが\(2\times 6\times \pi=12\pi\)であることを利用して 側面積は\(12\pi \times 5=60\pi (cm^2)\) よって、表面積は $$36\pi \times 2 60\pi=132\pi (cm^2)$$ となります。 体積は、底面積と高さを掛ければ良いから $$36\pi \times 5=180\pi (cm^3)$$ 那么圆柱的底面积公式就是圆形的计算公式 已知底面直径求底面积:(直径÷2)²×314 已知底面半径求底面积:半径²×314 a²=a×a 扩展资料: 圆柱的两个圆面叫底面,周围的面叫侧面,一个圆柱体是由两个底面和一个侧面组成的。 2圆柱体的两个底面是完全相同的两个圆面。两个底面之间的 Step3 「底面積」を2つと「側面積」を1つをたす!! 円柱の展開図をイメージしてみると、 「底面が2つ」+「側面が1つ」 になっていることがわかるよね?? だから、円柱の表面積は、 (底面積)×2 側面積 で求められるってこと!



三角锥形面积公式三角形的体积公式是什么 银颜网



1
〇 底面積は四角形の種類によって、面積の公式を使い分けてね! 四角柱の表面積 次の四角柱の表面積を求めなさい。 $$四角柱の表面積=側面積底面積底面積$$ 表面積とは、すべての面の面積をあわせたものです。 展開図をイメージすると簡単に求めることができます。 ポイントは以 この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h ってことは、こいつの面積は長方形の面積の公式をつかって、 (スキー板の面積) = タテ × ヨコ = ×100 = 00cm² になるね。 パスカルの計算では、面積の単位をm²に直さないといけないことに注意。 00cm²をm²に直してみると、 00÷ = 02 m² になるね。




圆柱表面积公式两个




直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com
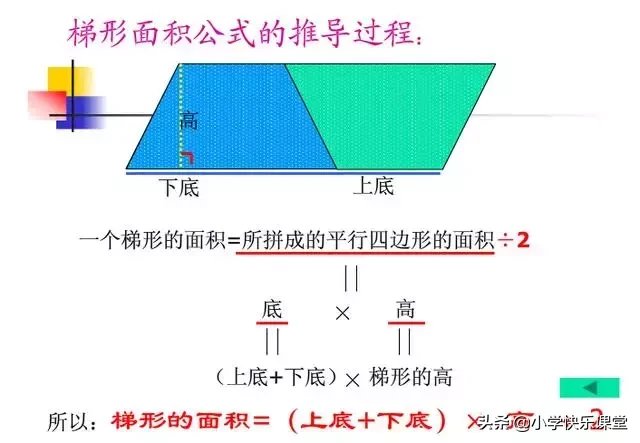
柱體體積=底面積×高 錐體體積=柱體體積÷3=底面積×高÷3 圓柱(正圓)體積=圓形(正圓)底面積×高=圆周率×底半径 2 ×高ネプリーグ ファイブリーグ不正解 台形の面積を求める公式 = ( 底下底)×高さ÷2 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't74 平行四邊形的面積公式 出自 高市資教中心教材網 前往: 導覽、 搜尋 五上74學習指引 math怎樣計算下圖平行四邊形的面積?/math math這個平行四邊形的底是6公分,高是4公分。/math math將平行四邊形沿著虛線剪開,拼成右圖的長方形。/math math拼成的長方形的長與平行四邊形的底



圆锥的体积周长面积公式




梯形面积计算公式
また底面積=7×7=49cm²であることが展開図よりわかります。 ここで、 四角錐の表面積=底面積+側面積 の公式より 側面積=四角錐の表面積ー底面積=1-49=140(cm²)であることがわかります。 7× ÷2=35 7× =70 よって =70÷7=10(cm)となります。底面積 S S S S 底面積 平面図形 公式 集 確認シート a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 四角柱 四角錐 三角柱 三角錐 円柱 円錐 空間図形 公式集 確認シート a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 Created Date 9/2/08 AM抛物线弓形面积公式等于:以割线为底,以平行于底的切线的切点为顶点的内接三角形的4/3,即: 抛物线弓形面积=S1/4*S1/16*S1/64*S=4/3*S 面积公式 长方形公式




小学数学图形的周长 面积 体积公式



Q Tbn And9gcrc0zk5rndihxchrex0elksjk4vngxujtpo6ofscvvgs5perp6k Usqp Cau
由於R是單位正方形,因此面積是一平方單位。將一平方單位代入R,得到:A1=lw1 將一平方單位代入R,得到:A1=lw1 A = l w {\displaystyle A=lw} (第五卷命題九)94 梯形的面積公式 出自 高市資教中心教材網 前往: 導覽、 搜尋 五上94學習指引 math怎樣計算下圖梯形的面積?/math math這個梯形的上底是12m,下底是6m,高是8m。/math math將上圖的梯形做一個全等的梯形,並與原梯形拼成平行四邊形,如下圖。/math math拼成的平行四邊形的底與梯形下の三角柱の体積を求める問題では、 どこが底面積 で どこが高さ かを考えさせることが大切です。 底面は必ずしも底にあるとは限りません。 上の場合は、横に2つある三角形の面が底面です。 下のように方向を変えて見るとわかりやすいでしょう。 求め方は、底面積×高さ なので 三角形の面積の公式から (底辺×高さ÷2)×高さ = (5×6÷2)×12=180 答え180




圓柱體體積圓柱體積怎麼算 從圓面積的概念找靈感 親子天下 Cuya
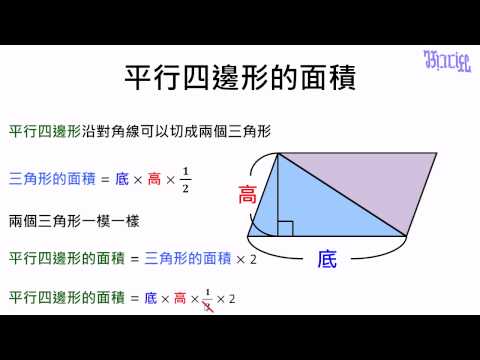



觀念 平行四邊形的面積計算方式證明1 數學 均一教育平台
のような変形は底の変換公式とは関係なく,それ以前に登場する対数の変形です. この公式 の特別な場合として もしくは,この公式 の特別な場合として と考えます. これらの前処理を行ってから,次に底の変換公式を使うことになります.(即組合後的平行四邊形面積÷2=梯形面積) (3)討論梯形與平行四邊形組成要素之間的關係(平行四邊形的底為梯形上下底的和),並引導出梯形面積公式。 (4)教師佈題,學生進行梯形面積的計算練習。 (五)透過觀察,讓學了理解四邊形面積=中線長×高== 底の変換公式 == 解説 底の変換公式 ** 記憶に残る覚え方 ** 格差社会 上の人はもっと上へ 下の人はもっと下へ ≪1教科書などに書かれているメジャーな証明≫ ≪対数の定義≫ 指数関数と対数関数の関係 (指数の形) (対数の形) (1)とおくと が成り立つ ≪対数をとるとは≫ 対数を「取っ
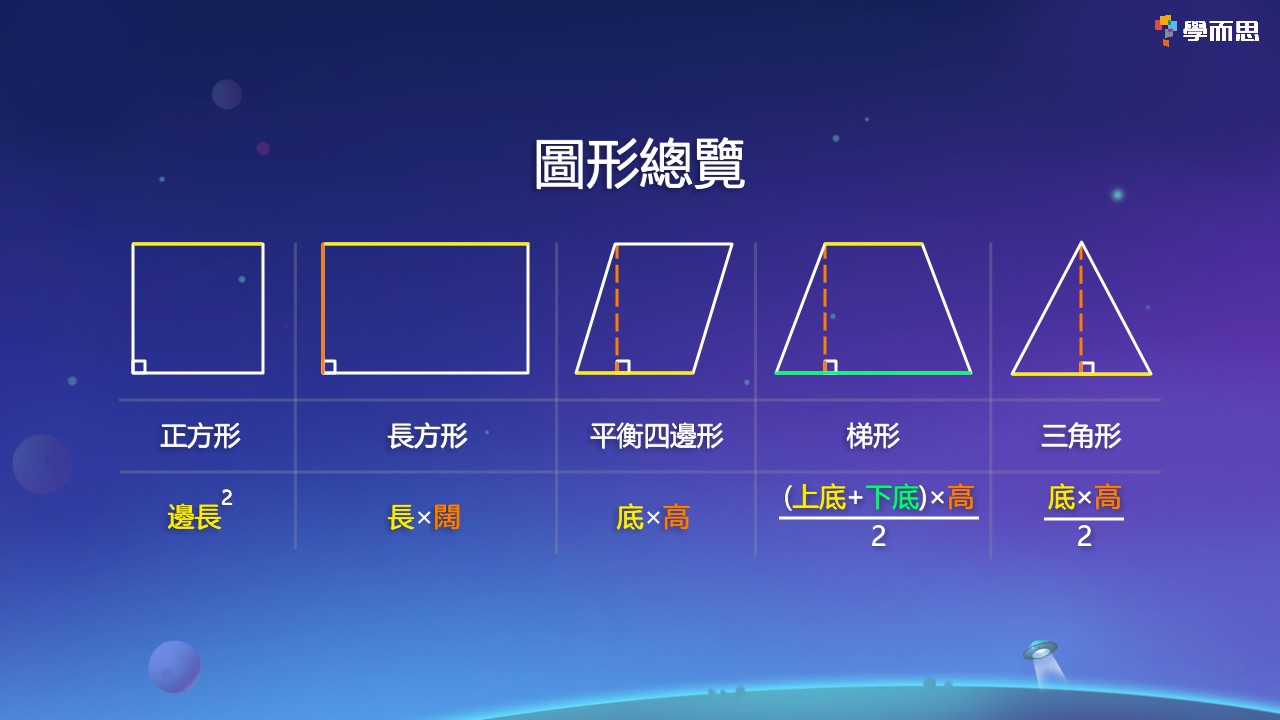



呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港




7 2 空间几何体的表面积和体积 Ppt Download




面積 29 求梯形的 底 的基本練習 Youtube



图文版 小学数学图形的周长 面积 体积公式 圆柱
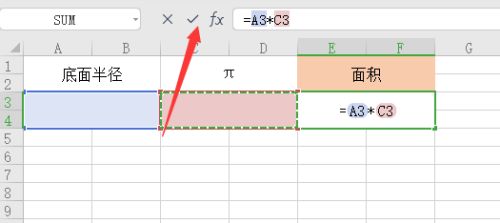



圆锥底面积公式怎么算 百度经验




十七种三角形面积公式



1



所有体积公式大全数学面积体积公式 朵拉利品网



Cuhkbmedtp Files Wordpress Com 16 07 Supplementary Note For Student Math1 07 Pdf



體積公式 台灣word




北师大版高中数学 面积公式和体积公式的简单应用 Ppt课件 牛图文



三角锥形面积公式三角形的体积公式是什么 银颜网



圓錐體積公式證明圓錐 Lvnmk
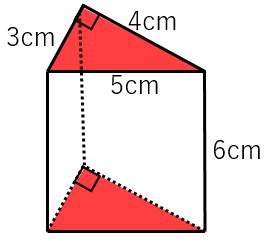



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学



底面积是什么 扒拉扒拉



圆锥体的面积公式 文章阅读中心 急不急图文 Jpjww Com



梯形体积公式梯形体积公式 一加一



圆柱公式 万图壁纸网



Cuhkbmedtp Files Wordpress Com 16 07 Supplementary Note For Student Math1 07 Pdf




斜棱柱体体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com




底面積 底面積的公式 圓柱的底面積 中文百科全書




57kytviwpv2qwm



正四棱锥表面积公式 正四棱锥底面积公式 七月seo



圆锥体的面积公式 文章阅读中心 急不急图文 Jpjww Com



底面积 快懂百科




怎么计算三角柱的表面积 生活百科
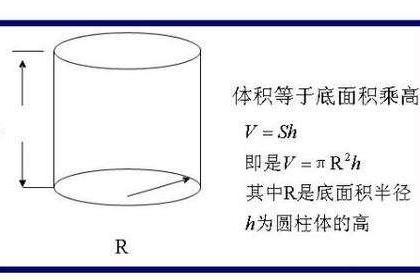



圆柱体积公式 搜狗百科




體積公式 體積公式 即計算各種幾何體體積的數學算式 華人百科




圆锥底面积公式用字母表达 圆锥的底面积公式是什么 三人行教育网 Www 3rxing Org



长方体 正方体 的体积 底面积 高v Sh Page18 苏教版六年级数学上册电子课本 教材 教科书 好多电子课本网




重要的底面積 每日頭條




圆柱体的体积怎么求 圆柱的体积公式 有图有真相




高中數學易錯點 重難點系列之 巧記空間幾何體的面積和體積公式 每日頭條



百科 百科 字典 成语 找字 生命树 文字通 智慧树 汉英 英汉 互译 时光隧道 朝代 国度 今日是何年 诗书伴读 中外诗歌 小说 历史 百科 散文 旅游 剧作 我的 用户 密码 登陆 注册 English 简体 繁體 Pinyin 图片 我的地图 北美枫文集 似曾相识 中外诗歌 小说 历史 百科 散文



什么叫圆柱体面积公式是什么 初三网



圆锥公式大全圆锥的全部公式 朵拉利品网



五年级数学 多边形面积公式推导全过程 灵活记公式 轻松解难题 算法之家




圆柱周长怎么算底面积 底面周长怎么求底面面积 已经圆的底面积求周长




4种方法来计算三角柱的表面积
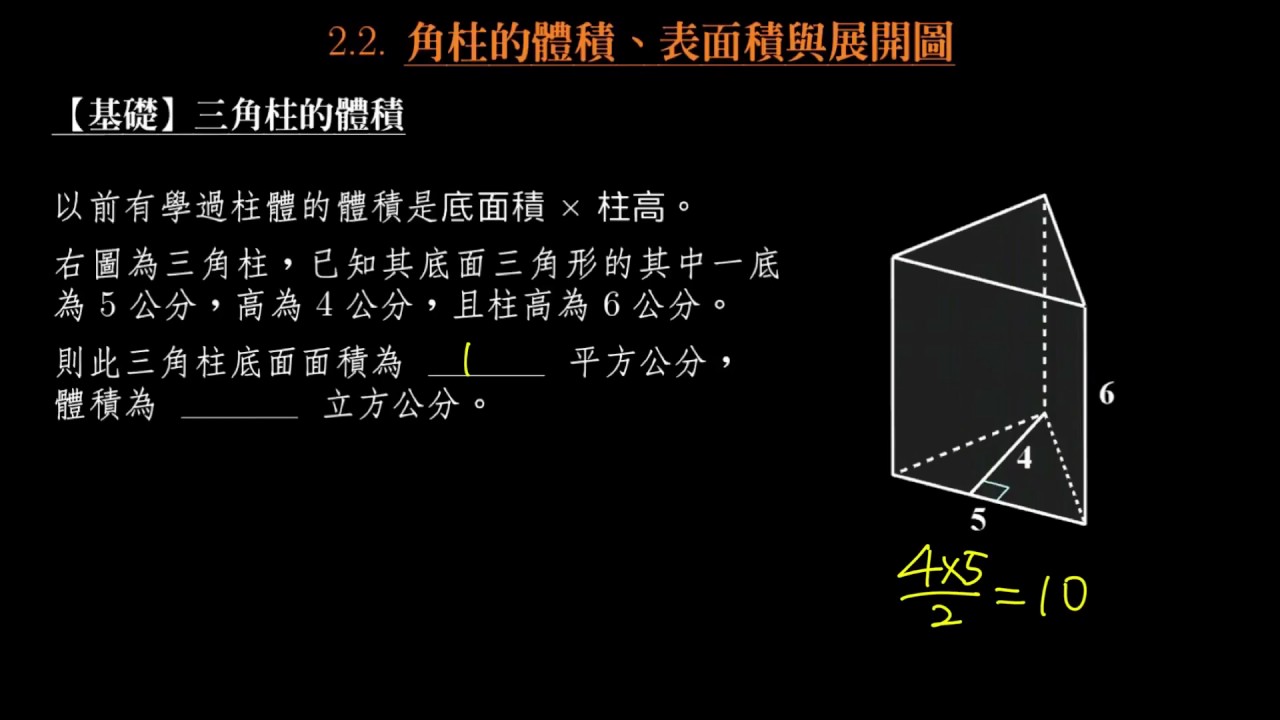



基礎 三角柱的體積 Youtube



1



圆锥的底面积公式是什么圆锥的底面积公式是什么 朵拉利品网
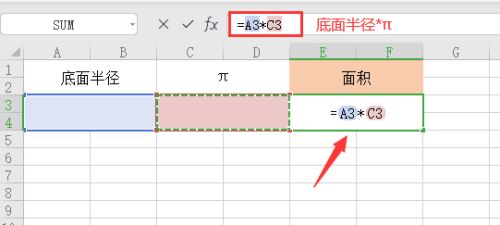



圆锥底面积公式怎么算 百度经验




圆柱的体积 圆柱和圆锥ppt课件2 Ppt课件下载 人人ppt



圆柱的面积公式 万图壁纸网



11 面積及體積 Area And Volume 齊齊溫




小学数学图形的周长 面积 体积公式




体积计算公式 面积公式 四棱台体积公式图解



圆锥的体积周长面积公式



三年级数学平面图形的周长 面积公式汇总 小初高题库试卷课件教案网



圆锥体积怎么算圆锥体积计算公式 朵拉利品网



关于底面积的体积公式 哔哩哔哩 つロ干杯 Bilibili



长方形的底面积 表面积 体积公式 作业 慧海网



圆锥侧面积公式2 信息评鉴中心 酷米资讯 Kumizx Com




Ppt 第五單元面積powerpoint Presentation Free Download Id



Ibg Mcrsrqa6um




计算




周长面积公式
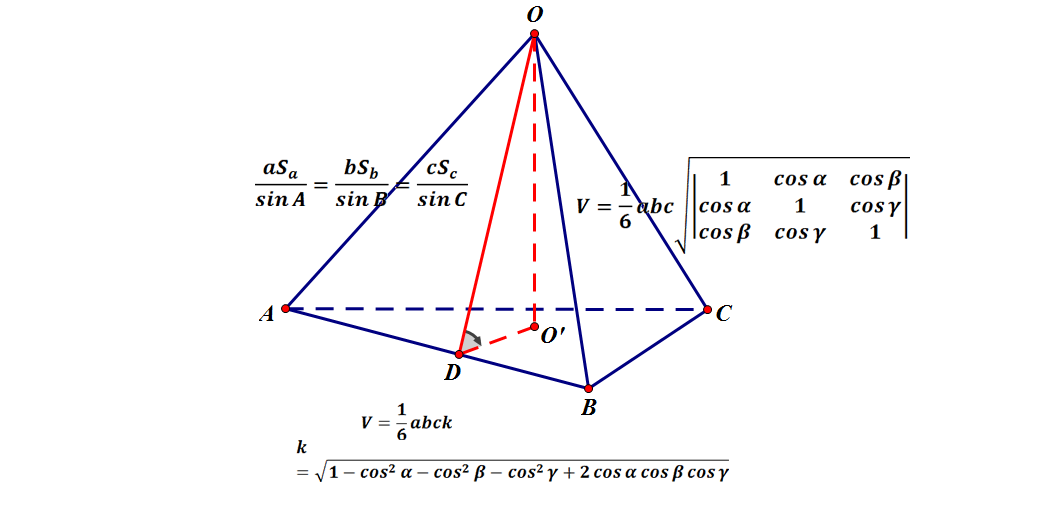



四面体体积公式 知乎
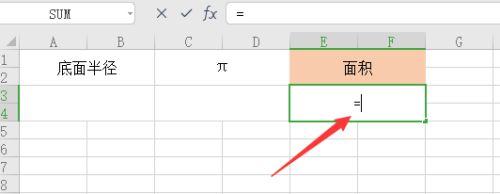



圆锥底面积公式怎么算 百度经验



图形面积体积公式大全 万图壁纸网




长方形底面积公式 西瓜视频




小学数学图形的周长 面积 体积公式 孩子学习必备 楠木轩



锥体面积计算公式体表面积计算器在线 减肥 减肥吧



圆柱的底面积公式中文 搜狗图片搜索




小学数学公式 圆柱的侧面积 表面积和总体积 爱学学习资源网



圆柱的底面积圆柱的底面积公式



Jq3mqygfpkb26m
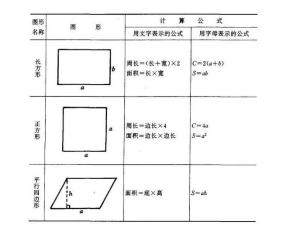



面积公式 搜狗百科




正方體面積立體形體 Mtlpe




长方形正方形面积公式推导 长方形的面积公式是怎样推导出来的 三人行教育网 Www 3rxing Org




面積 27 求三角形的 底 的基本練習 Youtube




油罐拱顶面积怎样计算 油罐拱顶表面积计算公式表达式底面积 35 784 拱高 0 739 求拱的表面积 三人行教育网 Www 3rxing Org




体积公式面积公式 雨露学习互助



体积公式 快懂百科



圆锥侧面积公式2 信息评鉴中心 酷米资讯 Kumizx Com




写给5年级的学生 球公式是如何推导出来的



三棱柱底面积公式 三棱柱的底面积公式 桃丽网




正六棱柱底面积公式推算 正六棱柱的底面积怎么求 正六棱柱的体积公式




长方截锥体上底面积公式




呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港
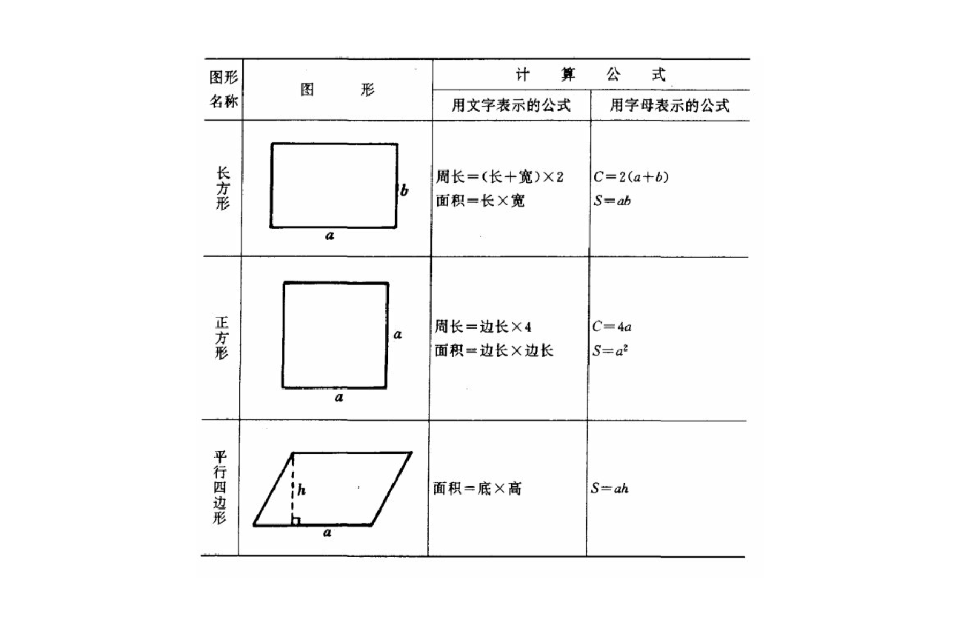



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



梯形面积公式求下底 不规则求梯形面积公式求不规则梯形的面积的公式 尚书坊



Cuhkbmedtp Files Wordpress Com 16 07 Supplementary Note For Student Math1 07 Pdf




柱體的體積與表面積 05 另一種長方形體積的計算方式 底面積x 高 Youtube




底面積 底面積是數學用語 一般用于求幾何體的底部面積 華人百科



长方体的表面积公式 信息阅读欣赏 信息村 K0w0m Com




底面積 底面積是數學用語 一般用于求幾何體的底部面積 華人百科




體積公式參考 Geogebra



细品教材 08年北京奥运会的重要前奏是奥运圣火的传递 圣火由 祥云 火炬承载 传遍五洲四海 宏扬奥林匹克精神 祥云 火炬外型是细长的圆台形式 长72 Cm 重985克 燃料为丙烷 那么在 祥云 的外层着色要覆盖多大的面积 其内部能盛装多少液态的丙烷 本节课



梯形面积公式 用2种拼组 2种分割 1种割补法




梯形面积公式是什么梯形面积怎么计算 传承网




长方形底面积公式 西瓜视频




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫



0 件のコメント:
コメントを投稿